Ponti

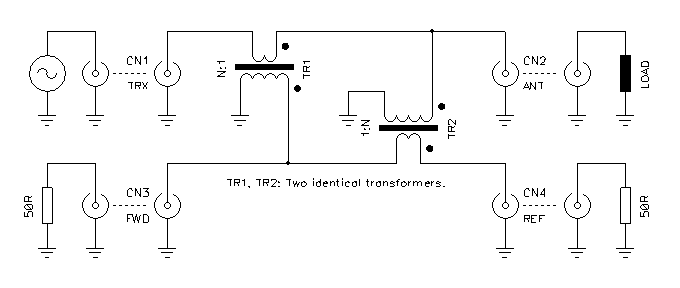
Tandem match (o Sontheimer)

In una linea di trasmissione, la corrente delle onde riflesse e' sfasata di 180° rispetto a quella delle onde dirette.

TR1 trasforma la tensione sulla linea di trasmissione in un segnale della stessa polarita' su CN3 e CN4.

TR2 trasforma la corrente sulla linea di trasmissione in un segnale di polarita opposta su CN3 e CN4.

• https://k6jca.blogspot.com/2015/01/building-hf-directional-coupler.html

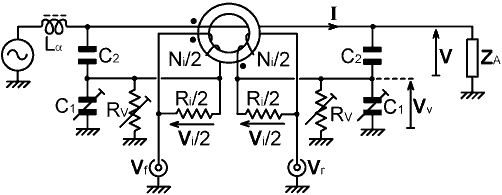
Douma (o Bruene)

Ponte di Wheatstone

Se si ha a disposizione un oscilloscopio a due canali, si possono misurare le caratteristiche dell'antenna usando un ponte di Wheatstone come questo:

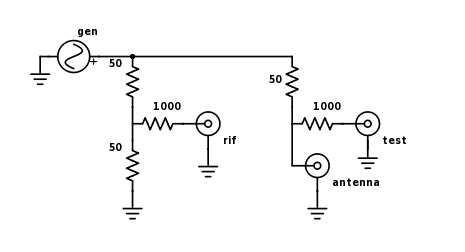
Le resistenze devono essere non induttive, di precisione almeno 1% e di potenza pari almeno a 1/4 del segnale iniettato.

Come generatore di segnale gen si puo usare il modulatore.

Le due porte rif e test vanno collegate con due cavetti di lunghezza e tipo identici ai due canali dell'oscilloscopio. Le entrate dell'oscilloscopio devono essere terminate con un impedenza pari a quella dei cavetti (ad esempio 50 ohm se si usa rg58).

Il segnale che esce dalla porta rif e' la forma d'onda prodotta dal generatore, mentre test e' lo stesso segnale applicato all'antenna da misurare.

• In condizioni ideali (antenna resistiva a 50ohm) i due segnali dovrebbero essere indentici (stessa fase e ampiezza).
• Se sono di ampiezza diversa, l'antenna ha una resistenza maggiore (test maggiore di rif) o minore (test minore di rif) di 50ohm.
• Se i segnali sono di fase diversa, l'antenna ha una reattanza capacitiva (test in anticipo rispetto a rif) o induttiva (rif in anticipo rispetto a test).

Per calcolare l'impedenza dell'antenna:

• T_delay = T_rif - T_test
• angolo di fase Φ: T_delay * f * 360
• per trasformare una impedenza R ∠ Φ da formato polare a formato rettangolare R + jX: R = R * cos(Φ), jX = R * sin(Φ)
• Zant = (50 * V_test ∠ Φ)/ (2 * V_rif - (R + jX))

ad esempio in python:

def wheatstone(Vref,Vtest,PHref,PHtest,Rrecref,Jrecref):
    # numeratore
    H2=Rrecref*Vtest
    I2=PHref+PHtest
    # print "num " + str(H2) + u' \u03C6' + str(I2)

    # denominatore
    H3=(2*Vref)-(Vtest*cos(radians(PHtest)))
    I3=(2*Vref*sin(radians(PHref))-(Vtest*sin(radians(PHtest))))
    # print "den " + str(H3) + " j" + str(I3)

    # forma polare
    I4=degrees(atan(I3/H3))
    H4=sqrt((H3**2)+(I3**2))
    # print "den " + str(I4) + u' \u03C6' + str(H4)

    Rpoltest=H2/H4
    Apoltest=I2-I4

    Rrectest=Rpoltest*cos(radians(Apoltest))
    Jrectest=Rpoltest*sin(radians(Apoltest))

    print "Zpol " + str(Rpoltest) + u' \u03C6' + str(Apoltest)
    print "Zrect " + str(Rrectest) + " j" + str(Jrectest)

wheatstone(Vref,Vtest,PHref,PHtest,Rrecref,Jrecref)